Jun 2011
Understanding Structural Response During Earthquakes Using Wavelet Transforms
As part of the development of performance based earthquake engineering, it has been determined that an important parameter in conducting a set of response history analyses is record-to-record variability. Record-to-Record Variability (RTR) is defined as the variation in response of a structure under multiple input ground motions that are scaled to a consistent ground motion intensity. The ATC 63 methodology summarized in FEMA P695 accounts for RTR variability by the number of ground motions, the types of ground motions, the scaling procedure, and a fixed value for the standard deviation of the lognormal collapse probability distribution used therein. However, the source of RTR variability is not well understood.
The causes of RTR variability are intimately tied to the way in which the earthquake ground motion and structural response vary in time. The primary tools that have traditionally been used for analyzing earthquake ground motions such as response spectra and Fourier transform do not provide any information about the variation in the signal over time. Wavelet transforms have been developed in the past three decades to analyze a signal’s frequency content through time using a variable resolution depending on frequency band. Wavelet transform methods are used in this project to analyze the time-varying frequency content of ground motions and structural response to quantify the sources of RTR variability.
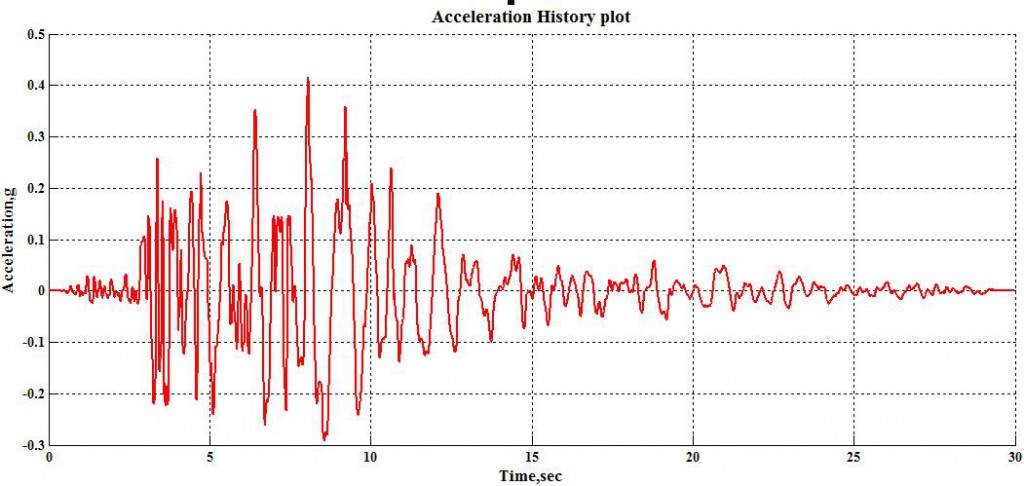
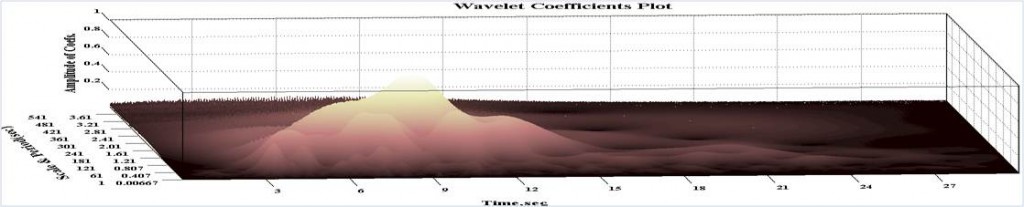
Ground motion accelogram from Northridge Earthquake as measured at the Beverly Hills (Top). Wavelet transform of the ground motion signal using Complex Morlet wavelets of bandwidth 1 and frequency 1.5.
Naga, P., and Eatherton, M.R. (2013) “Analyzing the Effect of Moving Resonance on Seismic Response of Structures using Wavelet Transforms” Earthquake Engineering and Structural Dynamics, Vol. 43, No. 5, pp. 759-768.
Naga, P. (2011) Analyzing the Effect of Moving Resonance on Seismic Response of Structures Using Wavelet Transforms, M.S. Thesis, Virginia Tech
More Research:
- Buckling Restrained Brace Subassemblage Testing
- Testing of Steel Crates
- Development of a Spectral Matching Algorithm
- End-Plate Moment Connections
- Self-Centering Beams for Resilient Earthquake Resistance
- Ring-Shaped Steel Plate Shear Walls
- Super High Tension Bolts
- Effect of Fasteners and Defects in the Protected Zone on the Performance of Moment Frames
- Controlled Rocking of Steel Braced Frames with Replaceable Energy Dissipating Fuses
- Development of a Self-Centering Buckling Restrained Brace
- Characterizing Hysteretic Behavior of Cold-Formed Steel Members and Connections
